Runz's Blog

SE-ML01-概要

定义

经典机器学习

学习是一个蕴含特定目的的知识获取过程。

  • 内部表现为新知识的不断建立与修正
  • 外部表现为性能改善

现代机器学习

任何通过数据训练的学习算法都属于机器学习

基本术语

归纳偏好

ML 算法在学习过程中对某种类型假设的偏好。这种偏好一定存在。

偏好最好与问题本身匹配，不然要用奥卡姆剃刀删掉。

NFL 定理

No Free Lunch 定理。一个算法 A 如果在某些问题上比另一个算法 B 好，必然存在另一些问题，B 比 A 好。

分类和回归区别

分类的输出是离散值，回归的输出是连续值。

评价指标

混淆矩阵、精度矩阵

精度矩阵是二分类下的混淆矩阵

精度矩阵下的名词

TRUE/FALSE: 预测结果与实际相符/不符

POSITIVE/NEGATIVE: 预测为真(阳性)/假(阴性)

算术指标

image-20240816164523881

  • Accuracy 精度

    • 预测正确的比例

  • Sensitivity 敏感率

    • 同查全率

  • Specificity 特异率

    • 阴性里预测正确的比例

  • Precision 查准率

    • 预测为阳性中真的阳了的比例

  • Recall 查全率

    • 所有阳性中预测出来的比例

统计学基本概念

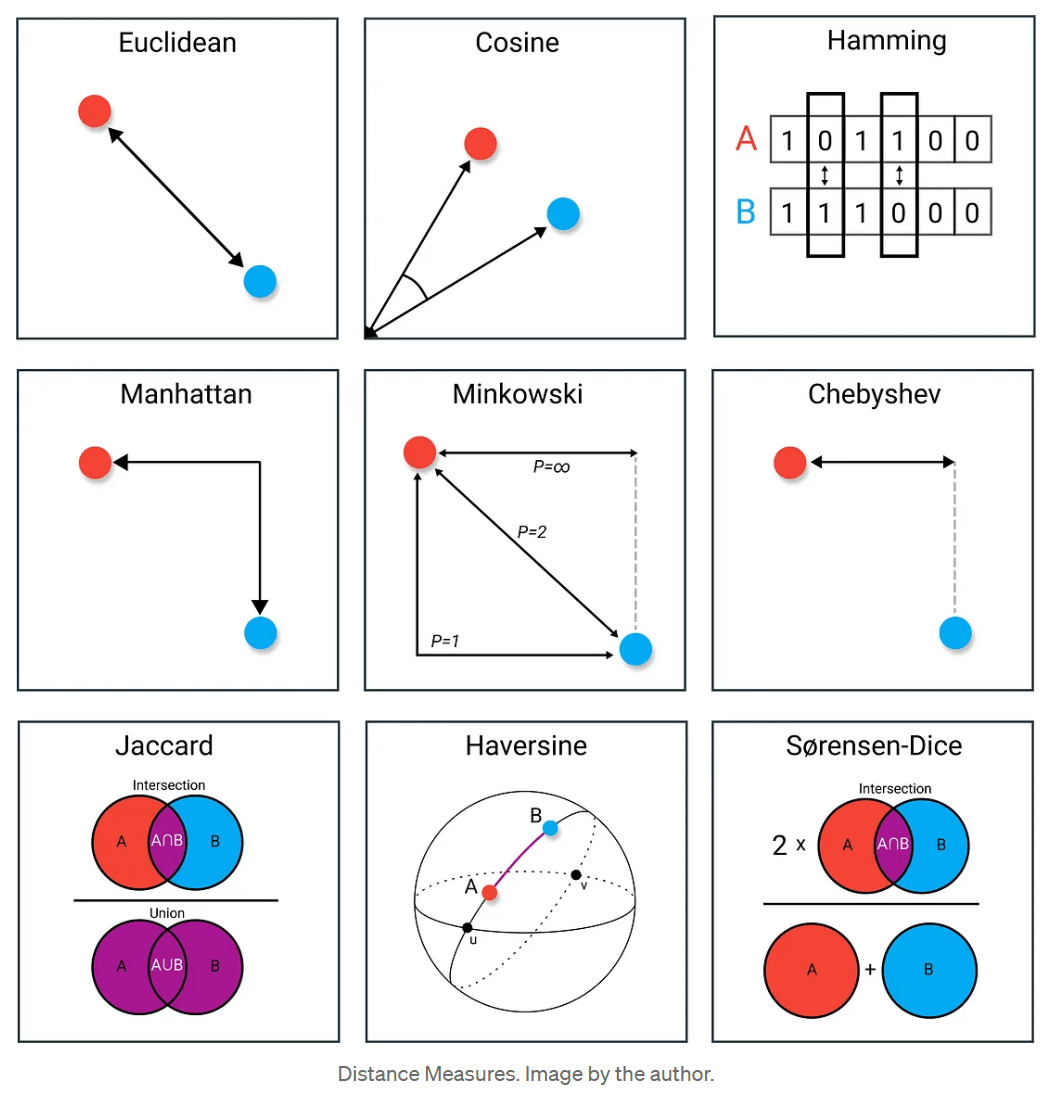
距离度量函数

对于两个样本 $x_i,x_j\in R^d$

  • 欧式距离 $d(x_i, x_j)= \sqrt{(x_i-x_j)^T(x_i-x_j)}=||x_i-x_j||_2$
  • 曼哈顿距离 $d(x_i, x_j)=||x_i-x_j||_1$
  • 切比雪夫距离 $d(x_i, x_j)=||x_i-x_j||_\infty$
  • 余弦距离 $d(x_i, x_j)=\frac{x_i^Tx_j}{||x_i||\ ||x_j||}$
  • 马式距离 $d(x_i, x_j)=\sqrt{(x_i-x_j)^TM(x_i-x_j)}$