SE-ML02-模型评估与选择

统计学习方法三要素

模型

在假设空间中的一个具体假设。是一个需要学习的函数。

策略

如何从假设空间中选择最优的假设/模型。

怎么判断模型优不优秀？损失函数与风险函数。

损失函数

评估 $f$ 在样本 $X$ 上，与真实值 $Y$ 的差距。

常见的损失函数：

• 平方损失函数 $$L(Y,f(X))=(Y-f(X)^2)$$
• 0-1损失函数 $$L(Y,f(X))=\begin{equation}\begin{cases}1,Y\neq f(X) \ \0,Y= f(X)\end{cases} \end{equation} $$

风险函数

经验风险：模型在训练数据集上的平均损失 结构风险：在经验风险的基础上，增加对模型复杂度，或者其他自定义惩罚

两种风险越低，模型越优。

算法

学习模型的具体方法。即损失函数或者风险函数的最优化问题。

有两种情况：

• 问题存在解析解，直接求解问题就可以得到最优模型
• 问题没有解析解，那就需要梯度下降、牛顿法这种方式去逼近最优解

最小二乘法就是存在解析解的问题，可以直接通过解方程求得使模型最优的参数。神经网络就需要不断通过梯度下降的方式更新权重。

评估方法

解决 “如何获得测试结果” 的问题

测试集与训练集的划分

留出法

将拥有的数据集，一部分划作训练集，剩下就是测试集。

注意：

• 保持数据分布一致性（分层采样）
• 多次重复划分（？没看懂）
• 测试集的比例，在 20% ~ 33% 间

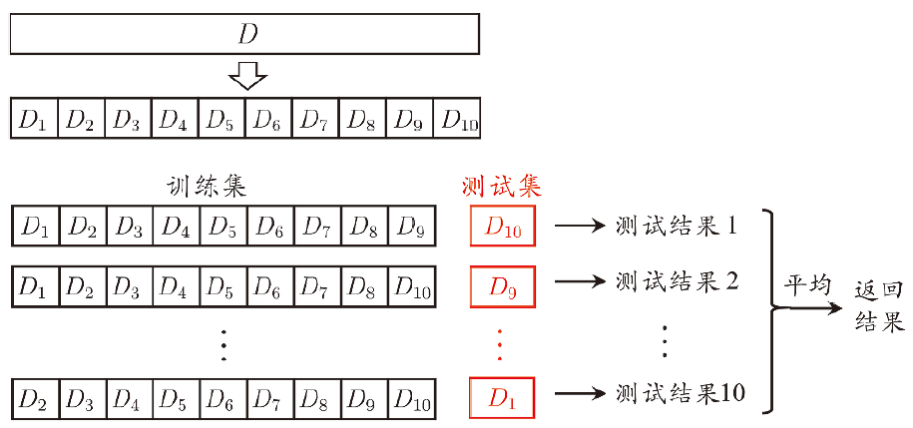
K-折交叉验证法

将测试集分为 K 份。进行 k 次训练。每一次按顺序选取第 i 份作为测试集，其他作为训练集。将 k 次的测试结果取平均，作为最终的结果。

自助法

一种可重复采样的方法。训练集和测试集可能有交集。

调参

在整个训练过程中，有两种参数：

• 算法的参数。就是超参数，使用验证集人工调参
• 模型的参数。由学习确定

在模型训练中，将验证集和训练集一起作为训练集。

性能度量

衡量模型泛化能力

均方误差

回归任务常用均方误差来评估：

$$ E(f;D)=\frac{1}{m}\sum_{i=1}^{m}(F(x_i)-y_i)^2 $$

错误率和精度

精度：

$$ acc(f;D)=\frac{1}{m}\sum_{i=1}^{m}II(f(x_i)=y_i) $$

其中罗马数字二 $II(expr)$ 是一个函数，用于将表达式 $expr$ 的布尔值转换为 0-1

错误率：不贴公式了，就是 1-精度

查全率和查准率

查准率（预测结果为正例中，有多少是 ground-truth）：

$$ Precision=\frac{TP}{TP+FP} $$

查全率（所有 ground-truth 中，多少被预测为正例）：

$$ Recall=\frac{TP}{TP+FN} $$

F1 score

综合查准率和查全率，得到的评估指标。

$$ F1=\frac{2\times Precision \times Recall}{Precision + Recall} $$ 如果对二者有不同偏好，可以加权重：

$$ F_\beta=\frac{(1+\beta^2)\times P \times R}{(\beta^2\times P)+R} $$ $\beta>1$ 时，更偏向查全率。

P-R curve

macro-micro

ROC, AUC

非均等代价

模型选择

如何比较模型

首先，不能根据上一步的性能度量，来直接评判模型优劣。因为性能度量是基于测试集的。

• 测试性能不等于泛化性能
• 测试性能随着测试集的变化而变化
• 模型本身就有随机性

使用统计假设检验来比较不同的学习器。

两个学习器之间

• 交叉验证 t 检验（基于成对 t 检验）
• McNemar 检验 （基于列联表，卡方检验）

多学习器比较

• Friedman + Nemenyi
  • Friedman 检验，基于序值，F 检验。判断是否都相同
  • Nemenyi 后续检验，基于序值。进一步判断两两差别