SE-ML03-线性模型

January 5, 2025

线性可分性

任意两个向量，分别属于两个类别。这两个向量和某个确定的权重向量的线性组合得到的标量值，如果一定落在某个标量值的两侧，那么这两个类别是线性可分的。

经典的二分类、线性、判别模型。

$$ f(x)=sign(\textbf{w}^T\textbf{x}+b) $$

$\textbf{w}$ 是平面的法向量，$b$ 是到原点位移。用这个超平面来判别。

高中数学知识

最小化均方误差。进行一堆最小二乘估计，得到最优解：

$$ w=\frac{\sum_{i=1}^{m}y_i(x_i-\bar{x})}{\sum_{i=1}^{m}x^2_i-\frac{1}{m}(\sum_{i=1}^mx_i)^2} \quad\quad b=\frac{1}{m}\sum_{i=1}^m(y_i-wx_i) $$

$$ f(x)=\textbf{w}^T\textbf{x}+b \quad 使得\quad f(\textbf{x}_i\simeq y_i) $$

求解思想是类似的，但是涉及矩阵求逆。

给线性组合加上一个单调可微的联系函数，这个联系函数可以是非线性的。

$$ y=g^{-1}(\textbf{w}^t\textbf{x}+b) $$

使用特殊的联系函数，使得输出满足 $y\in{0,1}$

$$ y=\begin{equation}\begin{cases}0,&z<0\0.5,&z=0\1,&z>0\end{cases}\end{equation} $$

性质不好，因为不是连续函数。不可微。

大名鼎鼎 Logistic function。高中生物里种群数量的 S 形曲线。

$$ y=\frac{1}{1+e^-z} $$

衍生出了 Logistic 回归。

以 Logistic 函数作为联系函数。

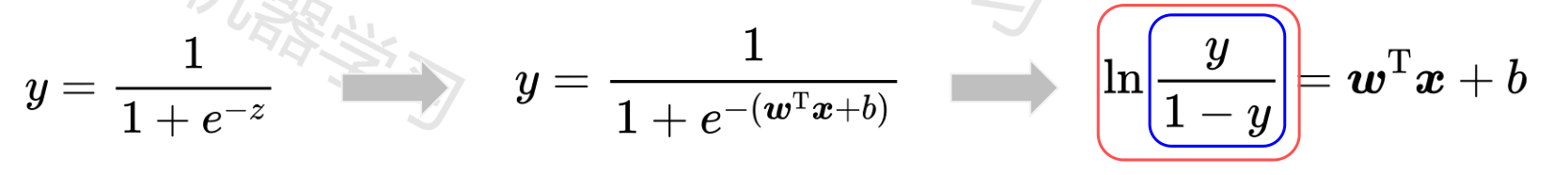
最后的 $ln\frac{y}{1-y}$ 称为“对数几率”。反映了 x 作为正例的相对可能性。

求解过程，是要最小化：

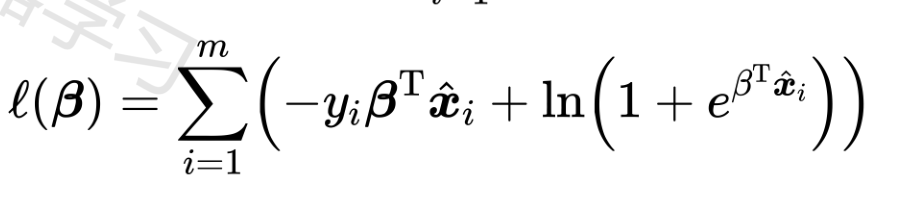
这是个高阶连续可导凸函数。可以用经典牛顿法等方法求解。

将一个线性回归模型，通过联系函数，转化成分类模型。

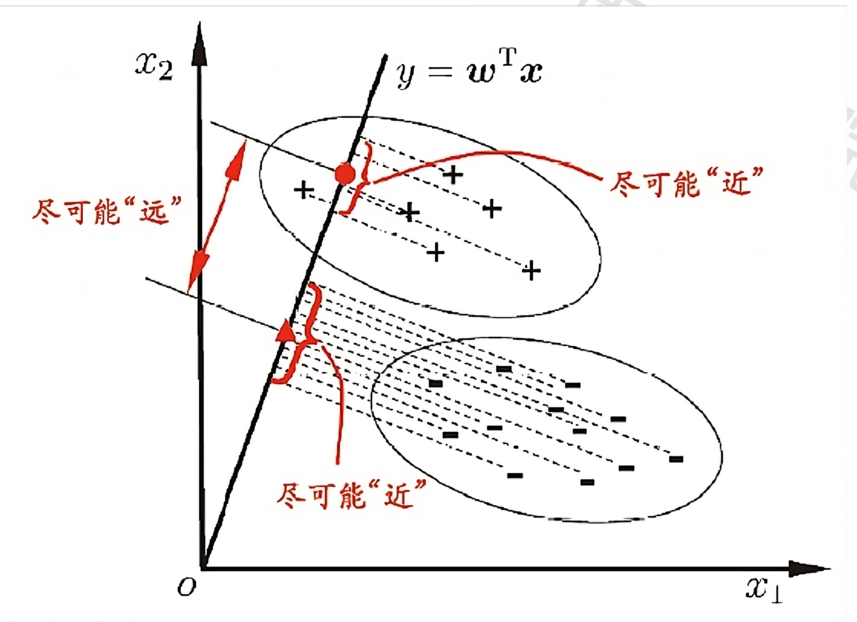
可以看作是一种监督降维技术。上图中把一堆二维的样本投影到直线上，完成了降维。

思想：将多分类拆成多个二分类任务。

OvO：每次只选取两个类，两类之间分类 OvR：每次选取一个类作为正类，其他全部作为反类