SE-ML06-支持向量机

线性 SVM

线性 SVM 最大化所有训练样本到决策平面的最小距离。

具有最小距离的样本，叫支持向量。

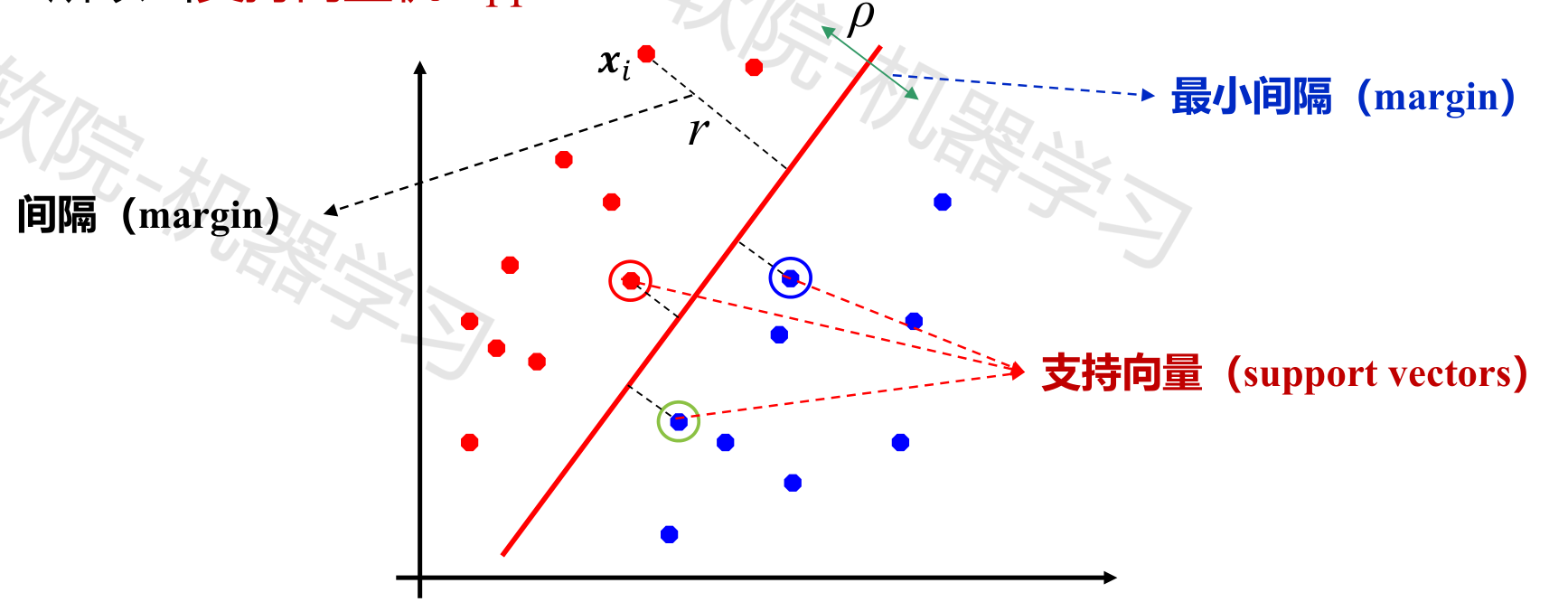
计算 margin

给定模型 $f(\textbf{x})=\textbf{w}^T\textbf{x}+b$，和任一样本 $x$ ，求其到超平面的距离 $r$。

$r=\frac{|f(x)|}{||w||}$

需要优化的式子出来了：

$$ \mathop{argmax}\limits_{\textbf{w},b}(\mathop{min}\limits_{i}(r_i)) $$

可以看到，这个式子的取值完全由间隔最小的样本决定。即模型的参数完全是由支持向量决定的。

分类

$f(x) > 0$ 分为正类，否则是反类。我们的目标就是让 SVM 尽量能完全分开两个类。

至于如何判断预测是否正确，如果正类的真实值是 1，反类是 -1 的话

$y_if(x_i)$ 为正值，预测正确。否则预测错误。

利用这个性质，需要优化的式子可以这样变，以保证 SVM 的可分性：

$$ \mathop{argmax}\limits_{\textbf{w},b}(\mathop{min}\limits_{i}(\frac{y_if(x_i)}{\textbf{||w||}})) $$

既考虑了预测的正确性，也考虑了最大化间隔的目标。

进一步优化

要优化的式子还是不够简单。我们从优化结果反着考虑：

假设我们最终得到的最优的模型的参数是 $(\textbf{w},b)$，考虑一个参数为 $(c\textbf{w},cb)$ 的模型，其中 $c>0$。

可以发现，这个新模型和最优的模型一毛一样

• 对于样本 $x_i$，二者预测结果一致。因为 $c$ 根本不影响符号
• 支持向量以及间隔不变，可以参考 $r$ 的公式，$c$ 都抵消掉了

所以，我们可以通过引入这个参数 $c$ ，使得要优化的式子更简单。

通过 $c$ 改变 $||w||=1$ 是一个不错的思路，但细想还是会发现，仍然比较复杂。

直接揭晓答案：通过 $c$，在约束 $\mathop{min}\limits_{i}(y_if(x_i))=1$，同时最大化 $\frac{1}{||\textbf{w}||}$。

拉格朗日乘子法

在约束条件下优化，可以用拉格朗日乘子法解决。

KKT 条件

对偶形式

和原始空间同时达到最优解。

soft margin

非线性支持向量机

通过引入类似线性模型中的联系函数，可以提高 SVM 的表达能力。

Kernel trick

类似联系函数的东西，能将低维特征映射到高维空间。