随记

Pumping Theorem的理解

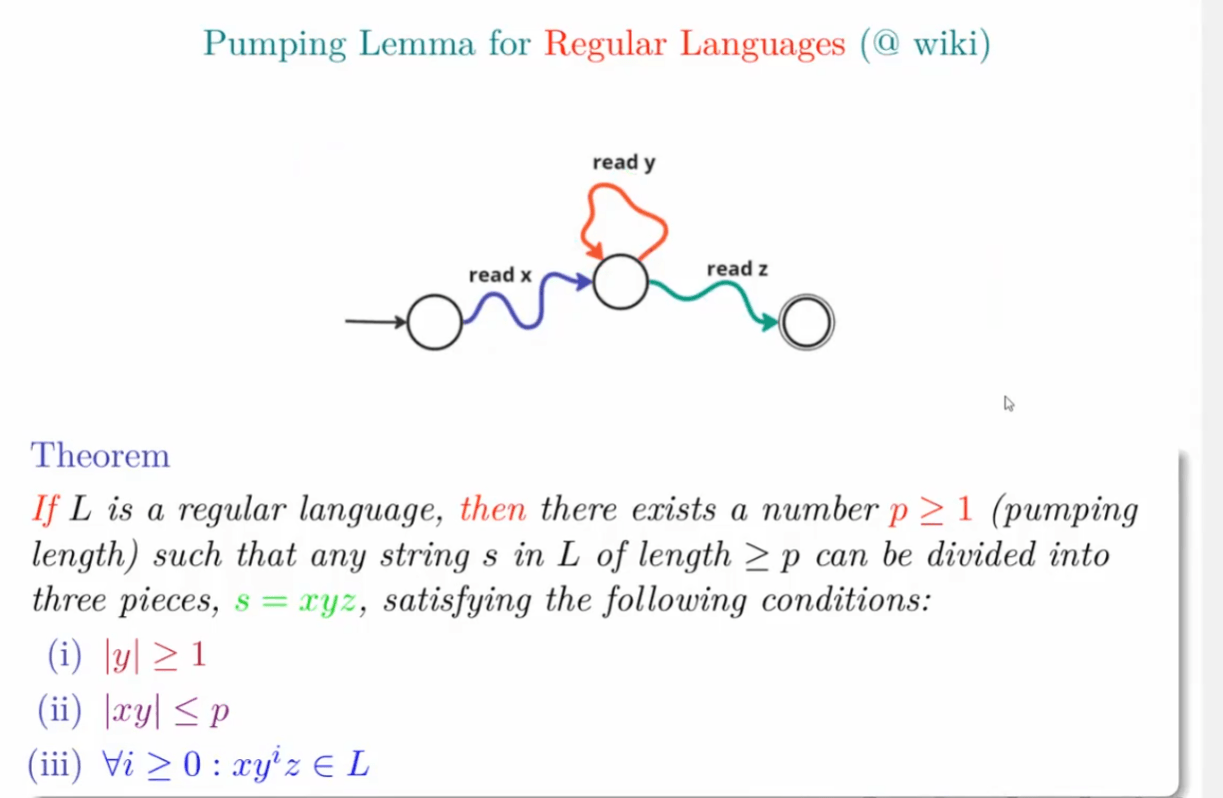
• 一个足够长的，能被正则表达式$r$接受的字符串，一定能分成$xyz$三个部分。因为$r$对应DFA的状态数$p$是有限的，而串的长度大于$p$时，一定有一个状态被经历了两次及以上

• 其中$y$对应$r$的DFA中起始状态和结束状态是同一个状态

• 由于是同一个状态，我就可以接受任意多个$y$，所以$xy^iz\in L$肯定成立

• 扩展：上下文无关法的Pumping Theorem，具体可见课件里面