04-测试用例优先级
回归测试
测试用例优先级是解决回归测试的一些问题的。
回归测试:版本迭代之后,重新运行之前的测试用例
但是,之前的测试用例:
- 用例庞大。太多了
- 用例冗余
- 用例失效。更新之后某些接口发生改变,原来的测试没法测
- 用例缺失。新的模块需要新用例
优化回归测试
要优化回归测试,就要优化测试用例集合。有如下方法
- 修复
- 选择⭐
- 扩充
- 缩减
- 优先级⭐
测试用例优先级 TCP
依照某种策略,给测试用例赋予优先级。优先级高的用例先执行。
即给定一堆测试用例,我们要确定一个用例序列,然后按顺序执行这些测试用例。
好处:提高测试用例集的故障检测率
流程⭐
- 特征提取。对特使用例进行特征表示
- 代码覆盖:语句、分支、函数
- 基于文本特征
- 基于缺陷特征
- 基于模型特征
- 基于 TCP 策略排序
- 贪心
- 相似性
- 搜索
- 机器学习
- 评估准则
- 错误检测率
- 时间开销
类型
通用测试用例优先级:版本越新,用例优先级越高 特定于版本的测试用例优先级:根据不同版本的特性分配优先级。爱怎么分怎么分。
⭐优先级策略
基于贪心的 TCP
基本是必考吧
贪心的对象一般来说是测试用例代码单元覆盖率。至于代码单元,有时候是语句,有时候是分支。
- 全局贪心:每一轮都选覆盖最多代码单元的测试用例
- 增量贪心:每一轮选覆盖了最多的当前还未覆盖的代码单元的测试用例
每一轮中,覆盖率相同的用例,随机选择。

基于相似性的 TCP
每轮优先与已选择测试用例集差异性最大的测试用例。让测试用例均匀地分布在输入域中。
定义两个用例 $t_1, t_2$ 间的距离:
$$ Jaccard(t_1,t_2)=1-\frac{|U(t_1)\cap U(t_2)|}{|U(t_1)\cup U(t_2)|} $$
就是两个用例覆盖代码的交并比。
而一个用例到用例集的距离,分别使用最大距离、最小距离和平均距离
基于搜索的 TCP
探索用例优先级排序组合的状态空间,以此找到检测错误更快的用例序列。
这个方法使用了遗传的思想。
- 种群构造。每一个个体是一个测试用例序列,比如我们随机生成两个个体:
表中的 1 ~ 6 是测试用例在个体中的顺序编号。

- 交叉(遗传)——染色体交换。选取一个交叉点,交换个体交叉点后部分的片段。为了保证 1 ~ 6 的一致性,我们不能直接交换数字,而是根据两段染色体中数字的相对大小来重新分配编号。见例图。
个体 1 中,5-2-6 在与 4-2-1 交换后,会根据 4-2-1 中的相对大小进行重排,得到 6-5-2

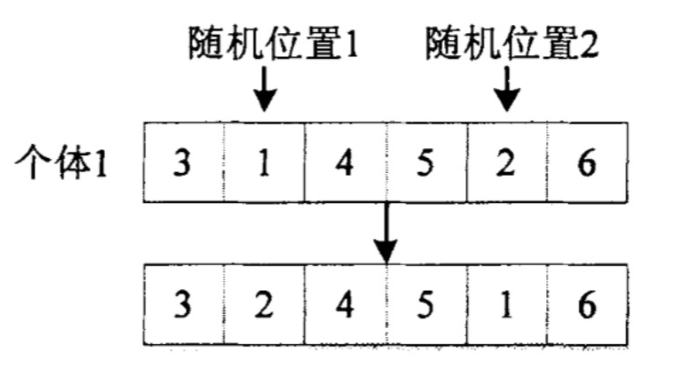
- 变异:随机交换两个编号。这一步是有一定概率发生的。
基于机器学习的 TCP
对测试用例特征进行学习,根据预测的缺陷检测概率进行优先级排序
- 特征提取。设计并提取测试程序中源码特征
- 缺陷模型生成,预测每个测试程序检测到缺陷的概率
- 开销模型生成,预测每个测试程序运行的时间
- 测试优先级
评估指标⭐
APFD⭐
包考的
平均故障检测百分比。
给定测试用例的执行次序,APFD 可以给出测试用例执行过程中检测到缺陷的平均累计比例。
有 $m$ 个故障 $F={f_1,f_2,…,f_m}$ 和 $n$ 个测试用例。$TF_i$ 表示给定测试用例执行次序第一个检测到故障 $f_i$ 的测试用例的下标。
$$ APFD=1-\frac{TF_1+TF_2+···+TF_m}{n\times m} + \frac{1}{2n} $$
APFDc
开销感知平均故障检测百分比。考虑了测试用例的执行开销和缺陷危害程度。
NAPFD
归一化平均故障检测百分比。
考虑了实际优先级排序场景中,
- 测试用例集不能检测到所有缺陷。
- 由于资源限制,无法执行所有测试用例
测试用例选择 TCS
旨在从已有测试用例集中选出所有可检测代码修改的测试用例
- 减少回归测试需要执行的用例数量,节约时间,降低开销
- 排除无关的测试用例,保留能暴露软件缺陷的,用最少的测试用例达到最大化缺陷探测能力的效果
方法概述
最小化测试用例选择
找出最小的子集,能覆盖本次版本修改影响的部分。
安全测试用例选择
选择能暴露变更后的代码中的缺陷的所有测试用例,构成安全回归测试集,集合中的用例满足以下条件之一:
- 执行至少一条被删除的语句
- 执行至少一条被新增的语句
基于数据流和覆盖的测试用例选择
选择能覆盖到变更代码中所有使数据交互变化的语句,构成测试集,满足以下条件之一:
- 执行至少一条被删除的 Define-use 对
- 执行至少一条新增的 Define-use 对
特质/随机测试用例选择
随机选。